取材・写真・文／大草芳江、資料提供／産業技術総合研究所東北センター

2021年08月31日公開

　大学や研究機関等で生まれた技術のシーズを企業の事業化に結びつける「橋渡し」機能を担う国立研究開発法人産業技術総合研究所（産総研）が、その橋渡し機能をさらに強化しようと、全国の大学敷地内に産学官連携研究拠点「オープンイノベーションラボラトリ（通称OIL）」を設置している。全国にある9拠点のうち、「材料科学」に「数学」の視点を導入し連携研究を進める東北大学材料科学高等研究所（AIMR）と連携し、同大敷地内に2016年に設置された拠点が「産総研・東北大数理先端材料モデリングオープンイノベーションラボラトリ（略称MathAM-OIL）」だ。数学を導入し新たな「材料科学」創出を目指すAIMRの研究基盤技術シーズと、産総研の「機能性材料コンピュテーショナルデザイン」研究機能を組み合わせ、次世代の先端材料を高速で開発し、産業界への橋渡しにつながる新たな研究領域の創出を目指すMathAM-OILの取組について、ラボ長の中西毅さんに聞いた。

※ 本インタビューをもとに、産総研東北センター展示スペースのポスター原稿を作成させていただきました。

【関連記事】
・2050年カーボンニュートラル実現にむけた技術革新とは？＜産総研化学プロセス研究部門インタビュー＞
・数学が切り拓く、新たな材料開発とは？＜産総研・東北大MathAM-OILインタビュー＞
・「技術を社会へ橋渡し」する産総研東北センターの産学官連携活動とは？＜産総研東北センター上席イノベーションコーディネータの南條弘さんに聞く＞
・日本初の国立デザイン研究所から始まった産総研東北センターの歴史とは

１．「数理先端材料モデリングオープンイノベーションラボラトリ」とは

－　「数理先端材料モデリングオープンイノベーションラボラトリ」が設立された目的は何ですか？

◆ 全国の大学内に産総研のラボを設置、基礎研究シーズを企業に「橋渡し」

　「オープンイノベーションラボラトリ」、通称「OIL（オー・アイ・エル）」は、経済産業省が「オープンイノベーションアリーナ構想」の一環として2016年度から始めた施策です。全国の大学内に産総研のラボをつくり、大学の基礎研究と、産総研の目的基礎研究・応用技術開発を融合し、企業へ「橋渡し」をするための産学官連携研究拠点として開設されました。

　全国に現在9拠点あるOILのうち3番目に設立されたのが、「産総研・東北大数理先端材料モデリングオープンイノベーションラボラトリ」、通称、「MathAM-OIL」です。2016年6月30日、東北大学片平キャンパス内に開所し、当時東北大学原子分子材料科学高等研究機構（AIMR）所長で数学者の小谷元子先生（現在・東北大学理事・副学長）と連携のもと、研究を推進しています。材料科学に数学の視点を導入し、世界に先駆けて新たな「材料科学」創出を目指すAIMRとの連携により、次世代の先端材料開発の高速化を目指しています。ちょうど今年6月に当初計画の第一期5カ年を終え、さらに延長が2025年3月まで認められたところです。

－　MathAM-OILでは、どのような研究を行っているのですか？

◆ 材料構造の隠れた秩序を見つけ、材料開発を加速化

　従来は「勘と経験」に基づく手法だった材料開発も、近年は「インフォマティックス（情報科学）」技術を活用した開発スピードの加速化が重視されています。例えば、アモルファス材料のように、原子や分子が規則的に並んでおらずぐちゃぐちゃに配列して、構造が一見無秩序な材料は、窓ガラスのみならず、金属ガラス（構造・磁性材料）やカルコゲナイドガラス（メモリ材料）、高分子ガラス（飛行機材料）など、様々な産業で利用されています。しかし構造が無秩序なために、周期性を有する結晶材料とは異なり、その構造を記述してモデル化する手法がなく、材料特性を計算・予測してインフォマティクスにのせることは非常に難しい問題でした。

　そこで、アモルファス材料の構造を記述し材料特性を予測することを、数学の理論で助ける「数理マテリアルインフォマティクス」を柱とし、材料開発の加速化を図ることが、MathAM-OILが目指すもののひとつです。

◆ 「無秩序の中の秩序」を、構造・機能・プロセスの視点から特徴づける

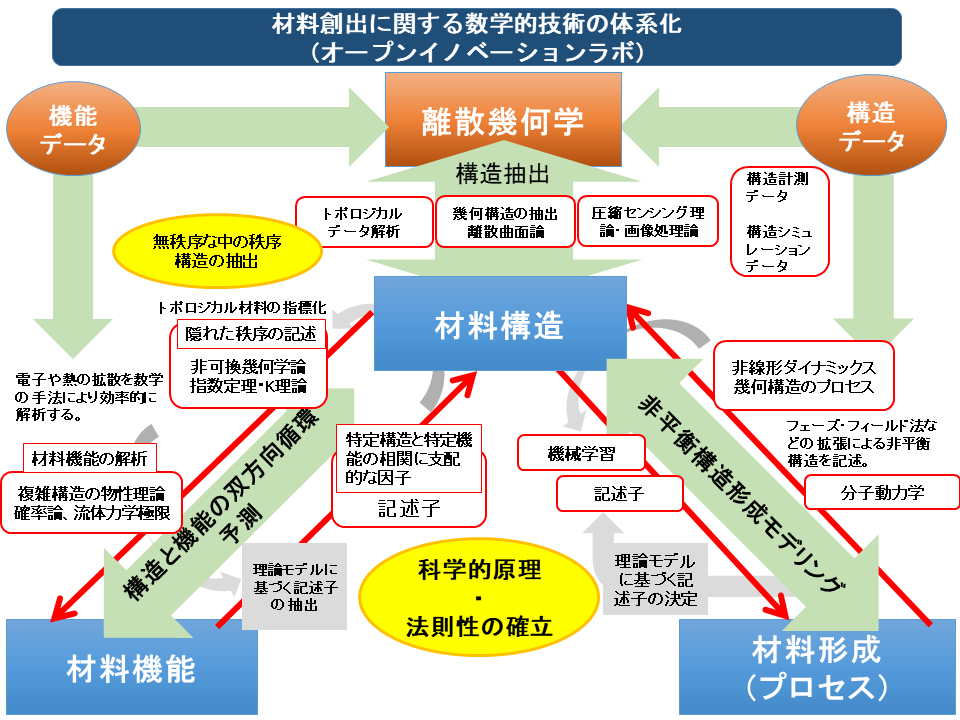
　構造の記述が難しい材料には、小谷先生のご専門である「離散幾何学」（「離散」は「連続」の対立概念。さまざまな形を離散的に捉えて幾何学として扱う新しい領域）という数学などを用いて構造を記述する研究を行います。材料の構造を記述できれば、材料の機能を計算（解析）できます。この問題は比較的簡単です。しかし企業様からのニーズは「こんな機能が欲しい、そのためにはどんな構造の材料が必要か」という逆向きの矢印である場合が多く、これは非常に難しい問題です。そこで、「記述子」と呼ばれる材料の特性を記述するパラメータの解明が必要になります。

　記述子とは、例えば材料のデータがぐちゃぐちゃとあった時、ある軸から見たら、綺麗に見えるという軸を与えるようなパラメータです。要求される機能から構造を読み解く場合だけでなく、材料形成（プロセス）についても、同様のことが言えます。モデリング、理論構築により記述子を抽出する研究を、我々理論、数学の研究者が頑張っています。

２．研究課題

－　MathAM-OILの具体的な研究課題について、ご紹介いただけますか？

　これまでの研究内容から説明しやすい話題をいくつか選んで紹介します。

　第一期は、「構造形成設計」「材料機能モデリング」「構造抽出」の３つを研究課題として研究を進めました。第二期では、より材料にフォーカスして、「ソフトマテリアル」「２次元材料」「アモルファス材料」の３つを研究課題として掲げています。

◆ 第一期の研究課題：データー解析、構造抽出技術の開発

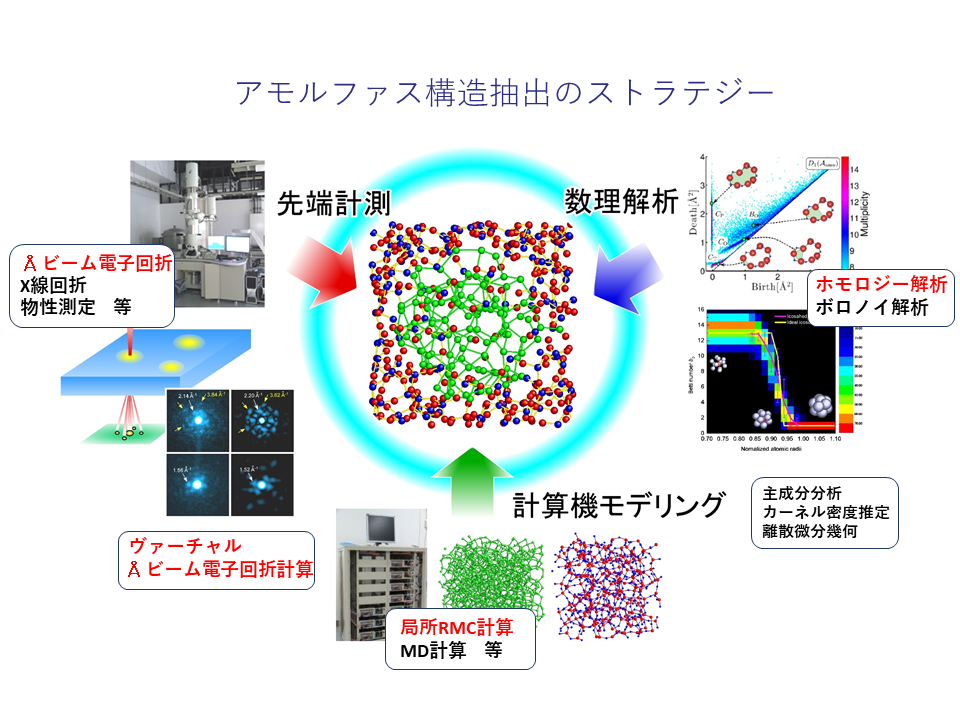
　第一期の研究課題は、簡単にご説明します。「構造抽出」では、アモルファスなどの材料の隠れた構造を抽出するため、電子顕微鏡を用いた観測と計算機シミュレーション、数学の手法を用いた解析を組み合わせた研究を行いました。ここでキーワードとなる「ホモロジー」という数学的概念を用いた解析については、後程ご説明します。

　「構造形成設計」では、高分子などのソフトマテリアル（金属や無機材料のように硬い材料に対して、高分子や有機分子など柔らかい材料の総称）の構造をシミュレーションし、形成プロセスを解明する研究を行いました。また、「材料機能モデリング」では、材料を「トポロジー」という数学的な概念を用いて分類し直し材料機能を予言する研究を行いました。これらについても後程詳しくご説明します。

－　「数学的概念を導入することで材料開発の加速化を図る」とは、具体的にどのような研究を行っているのでしょうか。具体例をひとつ挙げていただけますか。

◆ 「形」を定量化し材料の特性との関係を見つける
　 「パーシステント・ホモロジー」

　「パーシステント・ホモロジー」は、主な研究手法のひとつです。例えば、スタットレスタイヤに用いられる発泡ゴムには様々な形をした気泡が多数入っていますが、気泡の入り方とゴムの特性の関係は、企業からも関心の高いテーマだと思います。しかし、気泡の入り方のような無秩序な構造を記述するには、どうすればよいでしょうか？気泡の大きさについては従来も色々記述方法がありますが、気泡の形状や隣の気泡とのくっ付き具合も数字にして解析する必要があります。そこで、形を定量化する「パーシステント・ホモロジー」という数学の手法を用いた研究を進めています。「パーシステント・ホモロジー」はAIMRで開発された手法であり、最近では企業と連携した適用研究も進めています。

　「パーシステント・ホモロジー」は、穴が重要な材料に広く適用できます。例えば、発泡ゴムの他にも、ポリイミド・シリカナノコンポジット多孔体やガラス系多孔質ろ材など、色々な適用範囲があります。空胞に限らず、例えば合金はんだのように、カッパーとニッケルといった異なる元素が混じったもののどちらかを穴とみなすこともできます。また、不規則に並んでいる原子にも、パーシステント・ホモロジーを適用できます。

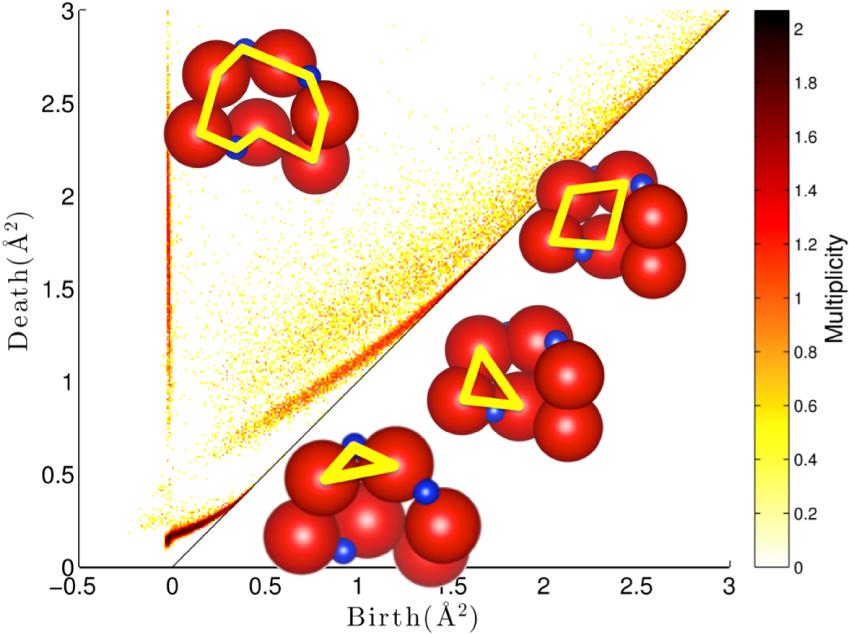【図】パーシステント・ホモロジーによるシリカの構造記述

　その時に何をするかと言うと、原子のまわりに円を書き、円の半径をどんどん大きくしていきます。そして円がお互いにつながって真ん中に穴ができた時を「Birth（バース）」と呼んでいます。さらに円の半径を大きくしていって穴が潰れた時を「Death（デス）」と呼び、グラフに点を打ちます（プロットします）。このようにして、ぐちゃぐちゃに並んでいる構造を、BirthとDeathの半径でプロットし数値化できます。２次元だけでなく３次元でも、また穴がつながっていることも、同じ要領で形状を記述（数値化）することができます。

◆ 第二期の研究課題：理論・解析技術によりデータ駆動マテリアル開発を高度化

（１）ソフトマテリアル

　第二期では、より材料にフォーカスして研究を展開します。自然界ではタンパク質や核酸などの生体分子が自発的に集まり、構造や機能を持つ組織になる「自己組織化」という現象がよく見られます。近年、高分子等のソフトマテリアルでも自己組織化で材料をつくろうという研究が行われています。すでに開発されている技術として、例えば、半導体デバイス製造時のフォトリソグラフィ工程において、自己組織化により微細な配線パターンを形成する技術はありますが、真っ直ぐ線を引くといった単純な構造です。そこでもう少し複雑な構造を、さらに夢としては人工血管や人工筋肉なども、自己組織化でつくれるようにしたいと研究を進めています。そのような欲しい構造がある時、どのような条件でどのようにソフトマテリアルを設計したらよいかを予測するために、「ベイズ推定」という統計理論の方法を用いて、方程式を推定する研究を行っています。

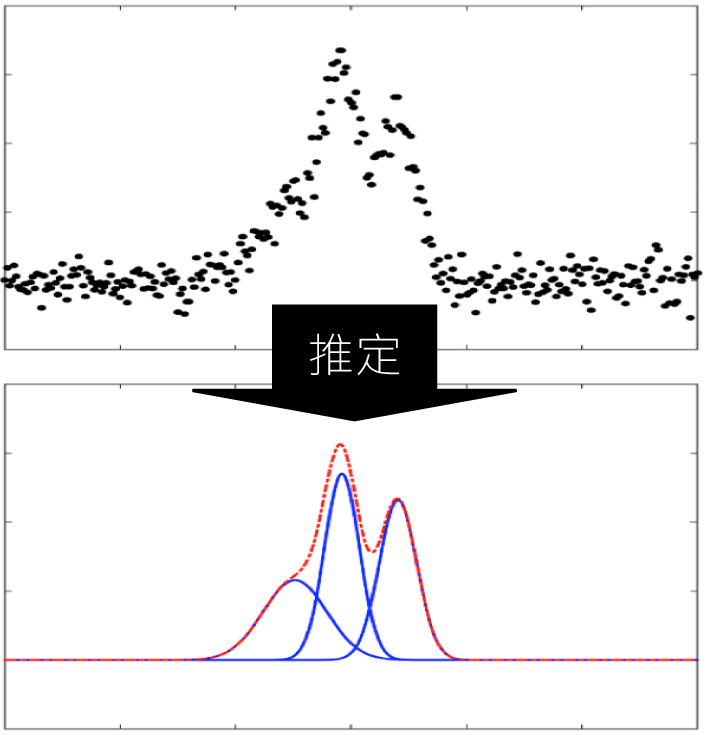
【図】ベイズ推定によるモデル選択。
測定で得られたスペクトルのデータ（上）から、ピーク関数のパラメータを推定した結果（下）。

　ベイズ推定に基づくデータ解析は、色々な場面で活用することができます。最も基礎的な使い方は、例えば、上図のようにノイズを含む実験データが与えられた時、普通は「これは３本のピークからなる」と目で判断してフィッティングしますが、ピーク数が２本ある時と３本ある時と４本ある時のどれが最も信頼性の高い解析になるかを、ベイズ推定に基づき、コンピュータで自動的に解析して、その信頼性がどれくらいかも含めてフィッティングする技術を開発しました。この手法を企業様のデータにも適用して共同研究も行いました。

－　「ベイズ統計」は最近、データ科学分野でよく聞くキーワードですが、それとはどんな関係や違いがあるのでしょうか？

　我々が取り組んでいるベイズ推定の研究は、計測データや計算データが少なかったり、ノイズが多くてぼやけていたり、とにかく情報が足りない時に、情報を補って解析するものです。例えば、ここに使えそうな理論式をひとつの情報として与えてやると、割とすっきりデータが整理できるのではないか。候補となる色々な理論式を試してみて、どれが尤もらしそうかを「推定」し、それが何十％くらい正しいかの信頼性評価に「ベイズの式」を使っているので、「ベイズ推定」と呼んでいます。

　このように理論式を使うことにより、データより外についても予言できる（外挿できる）ことが売りだと思います。最近流行っている「ベイズ最適化」も、ベイズ推定に基づいていますが、ここでやっている「ベイズ推定」とは少し違います。ベイズ最適化は、例えば、実験計画を立てる時、それまでの実験データの経験から、次はどこを測ればよいかがわかるので、効率的に実験やシミュレーションの計画を立てられることが、流行っている理由だと思います。ベイズ最適化は今まであるデータの範囲内で「この点をやりなさい」という内挿には強いけれど、その範囲外への外挿が難しいと言われています。

（２）２次元材料

　グラフェンに代表される原子層一枚あるいは数枚からなる「２次元材料（原子層材料）」が近年注目を集めています。また材料を「トポロジー」という数学の概念を用いることにより分類し直す研究も行っています。色々と変わった状態が出てくるので、それを将来の量子コンピュータに使えないかという研究も行っています。

　先程もお話したベイズ推定を用いたデータ解析は、東北大学の角度分解光電子分光（Angle-Resolved PhotoEmission Spectroscopy: ARPES）実験グループとの共同で、モデルを用いて2次元データをフィッティングする技術を開発しました。このベイズ推定を用いた新たな電子構造のデータ解析手法を高度化・汎用化し、2023年度から稼働予定の次世代放射光施設にも導入できたらと考えています。

―　計測したデータの解析手法は、企業からのニーズも高そうですね。次世代放射光施設が稼働すれば、ますますニーズは高まるのではないでしょうか。

　そうですね。理論や数学等のそれぞれの研究課題を進める中で、画像解析技術やモデル推定等、様々な数理的データ解析手法を開発してきた成果があります。次世代放射光の計測データ解析等にも適用していくことで、企業様の支援ができるのではないかと考えています。

（３）アモルファス材料

　アモルファス材料については、先程もご説明した「パーシステント・ホモロジー法」等を用いて、引き続き材料の複雑な構造を記述する研究を行います。

３．研究成果

－　これまでの主な研究成果についても、ご紹介いただけますか。

◆ アモルファス相変化記録材料の局所構造を抽出する局所逆モンテカルロ法を開発

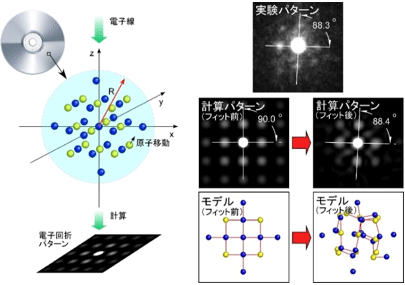【図】DVDなどの記録層であるアモルファス物質の局所構造をモデル化

　「構造抽出」については、電子顕微鏡とシミュレーションを用いて、アモルファス材料の構造を記述する方法を開発しました。電子顕微鏡で非常に狭い範囲を見ると、観察像は得られますが、それがどの構造に対応しているかわかりません。そこで、予想される構造をシミュレーションで多数作成し、その像と合うものを選ぶ、「局所リバースモンテカルロ法」という手法を開発しました。この手法を用いることで「この像はこんな構造です」とわかる成果が出ており、電池材料などへの貢献を期待され、企業様との共同研究を進めています。

－　「局所リバースモンテカルロ法」について、補足説明をお願いできますか。

　普通はより広い範囲を見て材料の構造を観察するのですが、この手法では電子顕微鏡の電子ビームをナノサイズに絞り（オングストロームビーム）、非常に狭い範囲で観察するので「局所」と呼んでいます。「リバース」は、普通はまず電子顕微鏡像があって、そこから構造を解析しますが、この手法では先に構造を予想してから像をつくり、その像と合うものを選ぶという逆向きの解析を行うため、「リバース」と呼んでいます。「モンテカルロ」は、乱数を使う計算手法を、業界用語で「モンテカルロ」と呼んでいます。とにかくサイコロをいっぱい振って構造の候補をいっぱい作成し、観察像をいっぱい得て、それと合致するものを選び出す手法です。それを全部合わせて「局所リバースモンテカルロ法」と呼んでいます。

◆ 自己組織化構造の形成と破壊を記述する数理モデルの構築（ソフトマテリアル）

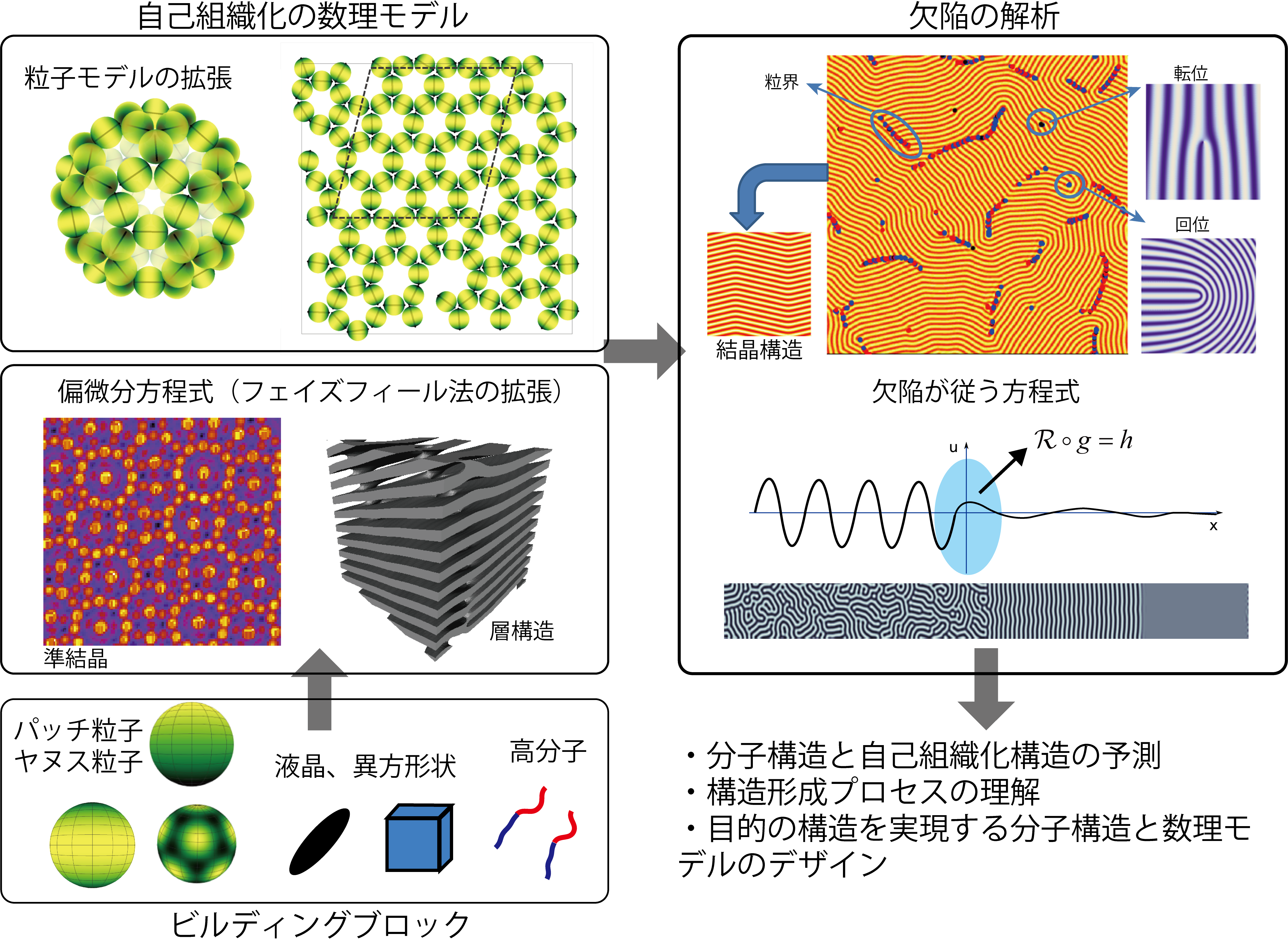
　自己組織化構造の形成過程の数理モデル開発については、先程も「自己組織化でつくれるソフトマテリアルの複雑な構造の設計」についてお話をしました。 「ヤヌス（双面）粒子」というもともと表面と裏面が違う「パッチ粒子」（例えば疎水性と親水性のように、表面に物性の異なる領域（パッチ）をもつ異方的なコロイド粒子）があった時、表面と裏面が違うため、自己組織化で勝手に組み上がっていきます。パッチ粒子があった時のシミュレーションのフレームワークをつくり、自己組織化の構造をシミュレーションできるようにしたのが、前期の成果でした。後期はそこに数理モデルを導入し、望みの構造をつくる研究を計画しています。

◆ トポロジカル量子コンピュータの材料となる高次トポロジカル絶縁体の予言

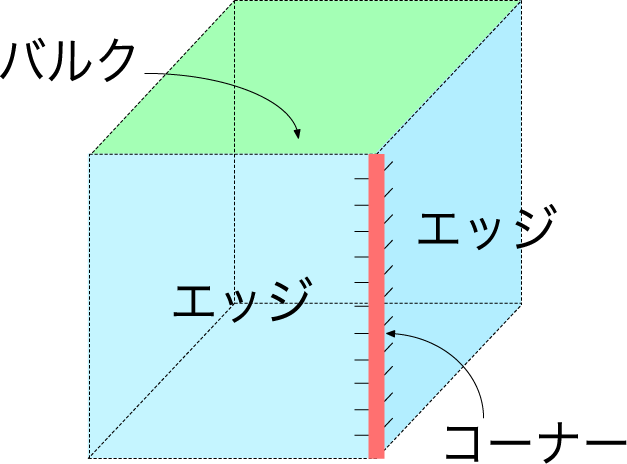
【図】高次トポロジカル絶縁体の理論

　「トポロジー」という数学の概念を用いて、材料を見直そうという研究も進んでいます。ラボの数学者が、端（コーナー）だけに金属状態が生じていて、その他は絶縁体の「高次トポロジカル絶縁体」を理論的に予言し、物理学者と一緒になって物理モデルを構築しました。このコーナー状態があることで、従来の量子コンピュータとは異なる新しい動作原理のトポロジカル量子コンピュータをつくれるのではないかと研究を進めています。

－　「トポロジカル絶縁体」も物理学で最近よく聞くキーワードですが、「トポロジー」や「トポロジカル絶縁体」についても補足説明をお願いできますでしょうか。

　トポロジーとは大雑把な形を認識する学問です。インターネットで「トポロジー」を検索すると、コーヒーカップとドーナッツの絵が出てくると思います。ドーナツもコーヒーカップも穴がひとつで、連続的にコーヒーカップを変形していくと、穴を潰したりつくったりしなくてもドーナツになりますよね。例えば、穴の数を数えるというのが、トポロジーという学問です。

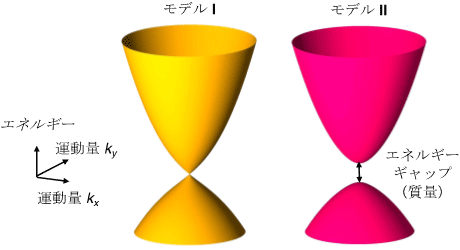
　理論物理の研究では、材料を調べる時、そのエネルギーと波数の関係を調べると一番基本的なことがわかります。そこで、エネルギーと波数のグラフを、多くの線で書くわけですが、線が交わっているか・離れているかが重要になります。その交わっているか・離れているかを記述するのに、トポロジーという概念が役に立ちます。いちいち波数とエネルギーの関係を計算するは非常に大変ですが、すべて計算しなくとも、トポロジーという概念を使うと、あるところだけ計算して、交わっているか・離れているかがわかります。上図のように、クロスしているのか（モデル1）、それとも上下で分かれているのか（モデル2）が、トポロジーを使うことでわかるのです。それを使って材料を分類しましょう、というのが最近の物理のトレンドです。

　また、最近流行っている「トポロジカル絶縁体」は、物質内部（バルク）は絶縁体なのに、その表面全部に電気が流れるのが、トポロジカル絶縁体です。

－　トポロジーを使って大雑把に形を認識することがどう有り難いかのイメージが湧きました。また、普通のトポロジカル絶縁体とは違って、この「高次」なトポロジカル絶縁体は、表面全部でなく端だけに電気が流れるのが特徴ということですね。それが従来とは異なる新しい量子コンピュータの実現につながるというのは、どういうことなのでしょうか。

　一次元の状態ができることがミソで、普通の超伝導体と一次元の状態の接合面に「マヨラナ」という最近話題の仮想的な粒子が出現します。これを使うと、量子コンピュータに応用可能と言われています。

－　ニュートリノの話で出てくるマヨラナ粒子ですか？（ニュートリノは、粒子と反粒子の区別がつかない特徴を持つマヨラナ粒子であるとする説が有力視されている。参考過去記事：http://shinbun.fan-miyagi.jp/article/article_20130601.php）素粒子のマヨラナ粒子が、材料科学や量子コンピュータとどう関係するのですか？

　そうそう、その通りです、そのマヨラナ粒子です。この一次元の状態というのは、ニュートリノと同じ方程式（ハミルトニアン）で記述されていて、その端に現れるのがマヨラナ粒子です。そのマヨラナ粒子を制御できると、不純物などの影響を受けづらいこの一次元の状態の性質を利用することができるので、ノイズに強い量子コンピュータの実現につながると言われています。

４．メッセージ

－　最後に、企業関係者に対して伝えたいメッセージをお願いします。

◆ ラボの出口は「産業数学」

　すぐに事業に結びつくかわからないような基礎的な研究に対しても、企業様から非常に関心を持っていただき、共同研究いただいているところもあって、非常に有り難いです。例えば、先程のパーシステント・ホモロジーやベイズ推定、データ解析等の手法は、比較的活用いただきやすいのではと考えています。実際、毎年ラボで主催している企業連携ワークショップにも、企業から多数ご出席いただき活発な議論をいただいています。

　我々のラボの出口は「産業数学」です。最近、日本の企業でも数学の活用に力を入れていたり、外国でも産業に数学を役立てたりする流れがあるそうです。これまで説明してきたような個々の技術の話ではなく、全体のフレームワークとして産業構造を革新的に変えるのが産業数学と理解されていると思います。

　数学の強さは、様々な範囲や対象に適用できる、そのユニバーサリティ（普遍性）です。パーシステント・ホモロジーを例に取ると、ゴム材料のように目に見えるものにも使えますし、アモルファス材料の原子・分子のように、電子顕微鏡でしか見えないものにも使えます。さらに材料に限らず、例えば社会問題など色々なところに使われています。そのような数学の新しい概念を軸とした、社会課題解決や産業育成への貢献が、産業数学に期待されていることと思います。そのような産業数学を一緒になって考えていきたいと思っております。

―　中西さん、ありがとうございました。